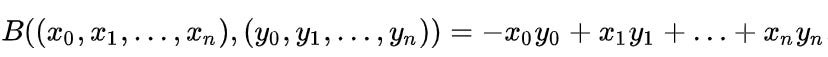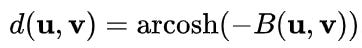2084: Hyperboloids and Minkowski

Minkowski Metric for Hyperbolic Space

So recently I started looking at hyperbolic neural networks, and thus I was wondering about embedding a point cloud into hyperbolic space. This was difficult as there’s a lot of models, but not many that work with just arbitrary n dimensional real numbers.

However after much research, I found the hyperboloid model. Now the hyperboloid model is essentially based on the following bilinear product of two lists:

This defines the distance between two points if they were placed on a sheet of a hyperboloid, a n dimensional analog of the 3 dimensional hyperbola

Now the distance is defined as:

This is easily calculable and is especially useful as a part of a loss for a neural network, since its so easily calculable. With some datasets, this is better than standard Euclidean distance since a lot of datasets lie on a hyperbolic manifold. There’s also some really cool work done on hyperbolic neural networks, which is well worth reading.